Come trovare il sostegno di una curva?

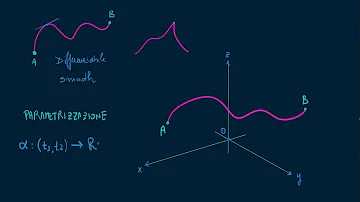
Come trovare il sostegno di una curva?

ha come sostegno il segmento che unisce il punto x al punto y. Il segmento sostegno di r viene spesso denotato con la scrittura [x, y]. si ha che il sostegno di ˜r `e una retta, in particolare la retta passante per i punti x e y. r = z + tv , t ∈ R.

Come capire se una curva è semplice?

Definizione 1.4. Una parametrizzazione ϕ(t) si dice semplice se a valori distinti di t corrispondono punti distinti, esclusi al pi`u gli estremi a e b dell'intervallo I che possono avere per immagine lo stesso punto. Una curva `e detta semplice se esiste una sua parametrizzazione semplice.

Come può essere una curva?

Una curva può giacere su un piano, nello spazio euclideo, o in uno spazio topologico più generale. Una curva può essere pensata intuitivamente come la traiettoria descritta da un oggetto puntiforme che si muove con continuità in qualche spazio.

Come si vede se una curva è regolare?

Un arco di curva si dice regolare a tratti se l'intervallo su cui `e definito si pu`o suddividere in un numero finito di sottointervalli in modo tale che su ciascuno di essi l'arco sia regolare. funzione regolare in I. ... Se tale estremo superiore `e finito l'arco di curva si dice rettificabile.

Come si fa la parametrizzazione di una curva?

Abbiamo una parametrizzazione semplice se a valori di (t) corrispondono dei punti diversi, esclusi gli estremi di "a" e "b" dell'intervallo L. La parametrizzazione di una circonferenza, invece, è possibile ottenerla attraverso lo studio del seno (sin) e del coseno (cos).

Come dimostrare che due curve sono equivalenti?

DEFINIZIONE. Si dice che due curve equivalenti (γ1,Γ1) e (γ2,Γ2), con γ1 ° ϕ = γ2, hanno lo stesso orientamento se и ϕ'(s) > 0, ∀s ∈ I2, mentre si dice che le due curve hanno orientamento opposto se и ϕ'(s) < 0, ∀s ∈ I2.

Quando una funzione è semplice?

In matematica, specialmente in analisi matematica, una funzione semplice è una funzione misurabile la cui immagine è finita.

Quali sono le curve coniche?

Queste curve si chiamano coniche perché sono ottenute tramite l'intersezione di una superficie conica con un piano. Si possono definire tutte come luoghi geometrici e, di conseguenza, ricavarne l'equazione algebrica che le rappresenta nel piano cartesiano.

Come si chiamano le curve nel piano cartesiano?

Nel piano cartesiano, la curva trascendente in coordinate polari : dove a è un numero positivo, è detta spirale di Archimede. Nel caso in cui a = 1 il grafico è : 06 – Spirale iperbolica.

Come capire se una funzione è regolare a tratti?

Definizione 2. Diremo che f è regolare a tratti se: è continua in [- , ) tranne al più in un numero finito di punti nei quali esistono finiti i limiti destro e sinistro; cioè per ogni i = 1, ..., N: ha derivata continua eccetto nei punti ed eventualmente in altri punti (sempre in numero finito); è limitata.

Cosa è una curva in matematica?

• In matematica, una curva è un oggetto unidimensionale e continuo, come ad esempio la circonferenza e la retta. Una curva può giacere su un piano, nello spazio ...

Cosa è una curva piana?

• Una curva piana è una curva a valori nel piano cartesiano. f : [ a , b ] → R 2 {\\displaystyle f:[a,b]\\rightarrow \\mathbb {R} ^{2}} Parametrizzazioni [ modifica | modifica wikitesto ]

Cosa è supporto o sostegno di una funzione?

• In matematica, il supporto o sostegno di una funzione è il sottoinsieme dei punti del dominio dove la funzione non si annulla. Se il dominio è uno spazio topologico ...